斐波那契数列，又称黄金分割数列，是一种递归的数列，以它的递推公式和美丽的数学性质得到了广泛的应用。本文将介绍使用 JS 实现斐波那契数列的几种方法，包括递归和循环，以及优化方案等。

1. 斐波那契数列定义

斐波那契数列（Fibonacci sequence）是一种递归的数列，以它的递推公式和美丽的数学性质得到了广泛的应用。它的定义如下：F(0)=0，F(1)=1，F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）。也就是说，第 n 个斐波那契数就是第 n-1 个和第 n-2 个斐波那契数之和。通常用 F(n)表示斐波那契数列中的第 n 个数。斐波那契数列是一个由 0 和 1 开始，后续的每一项都是前两项之和的数列。

2. 以终为始——递归实现

2.1 普通递归

对于普通递归我的总结就是：以终为始，套娃计算，适时终止。

  • 以始为终：用倒推的方式来思考。
  • 套娃计算：找到套娃的公式。
  • 适时终止：递归到能直接得到结果的地方就停并返回结果。

下面我们来开始倒推。从后往前倒推就是 :

1
2
3
4
5
6
f(n) = f(n-1) + f(n-2)
f(n-1) = f(n-2) - f(n-3)
...
f(3) = f(2) + f(1)
f(2) = 1
f(1) = 0

我们可以得到：

  • 公式：f(n) = f(n-1) + f(n-2)
  • 终止条件：n=2 和 n=1

最终代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
function fibonacci(n) {
    if (n < 1) return 0
    if (n <= 2) return 1
    return fibonacci(n - 1) + fibonacci(n - 2)
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
fibonacci(3)

JavaScript 代码运行时，函数调用会在内存形成一个“调用记录”，又称“调用帧”（call frame），保存调用位置和内部变量等信息。
F(50)调用 F(49) 和 F(48)，F(49)调用 F(48) 和 F(47)，…
以此类推，所有的调用记录，就形成一个“调用栈”（call stack）。
如果栈深度过大，就会导致堆栈溢出。

  • 测试一下你的调用栈
1
2
3
4
5
6
7
8
9
10
11
let i = 0;
function inc() {
  i++;
  inc();
}
    
try {
  inc();
} catch(e) {
  console.log('你的浏览器中最大的调用栈是：', i);
}

2.2 缓存重复计算

上面提到fibonacci(50)在浏览器中执行因为栈溢出会导致浏览器卡死的情况，让我们来优化一下。
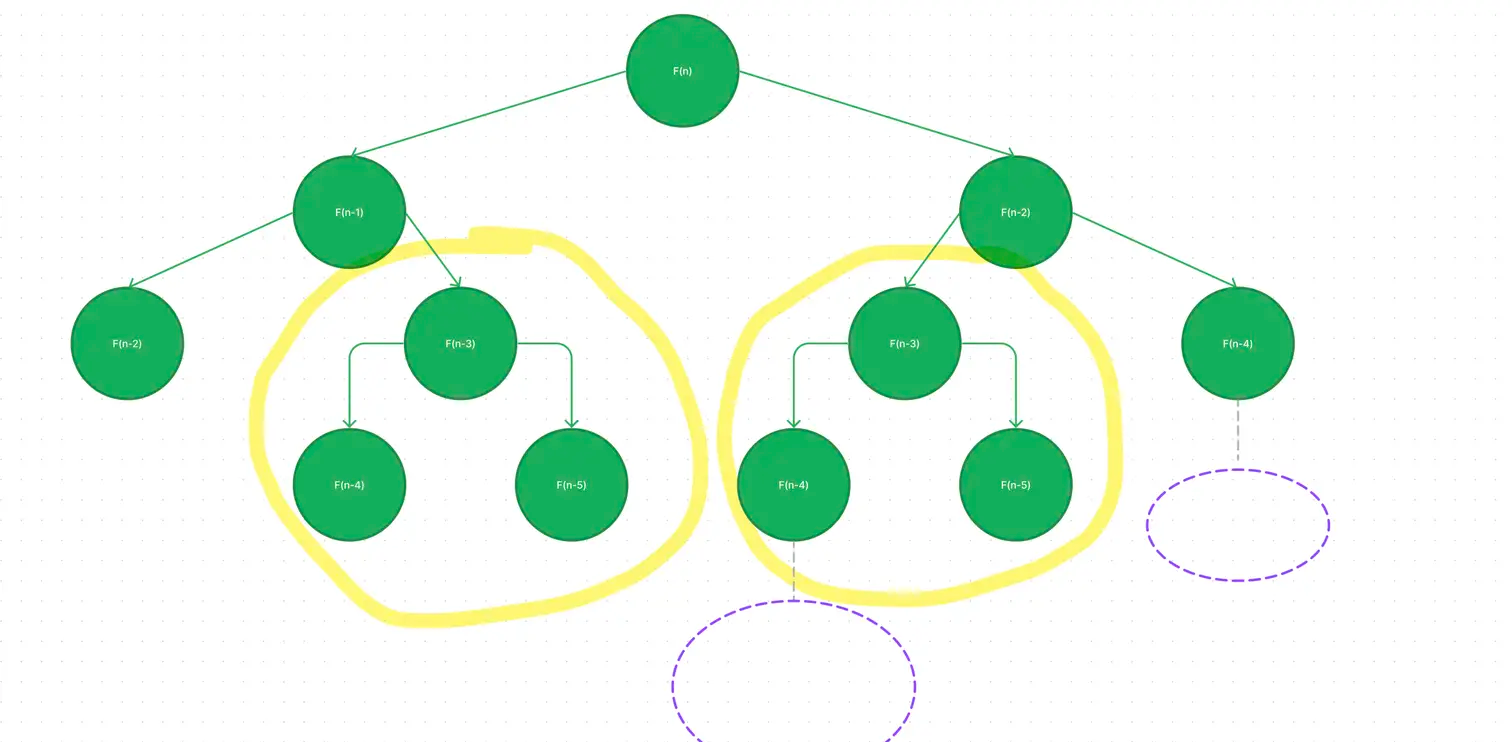
观察下图我们不难发现，两个黄色实线圈和两个紫色的虚线的地方，都出现了重复计算,fibonacci(n)中的 n 越大，重复计算的地方越多。如果我们能缓存每次计算的结果，就能减少重复计算，提升运行效率。

image-20230713154812257

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function fibonacci(n) {
  // 利用闭包缓存计算的结果
  const memo = [0, 1];
  function fib(n) {
    if (memo[n] === undefined) {
      return memo[n] = fib(n - 2) + fib(n - 1);
    } 
    return memo[n];
  }
  console.log(fib(n));
  return fib(n);
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
// ...
fibonacci(50)

2.3 避免重复计算（尾调优化）

尾调用优化是一种有效的优化技术，可以减少函数调用次数，从而提升递归函数的效率。它的原理是将当前函数的返回值作为另一个函数的参数，并将函数的调用放到最后（即尾调），从而减少函数调用和堆栈的深度。这样，就可以让函数能够在堆栈中以更少的深度运行，从而提高函数的效率。

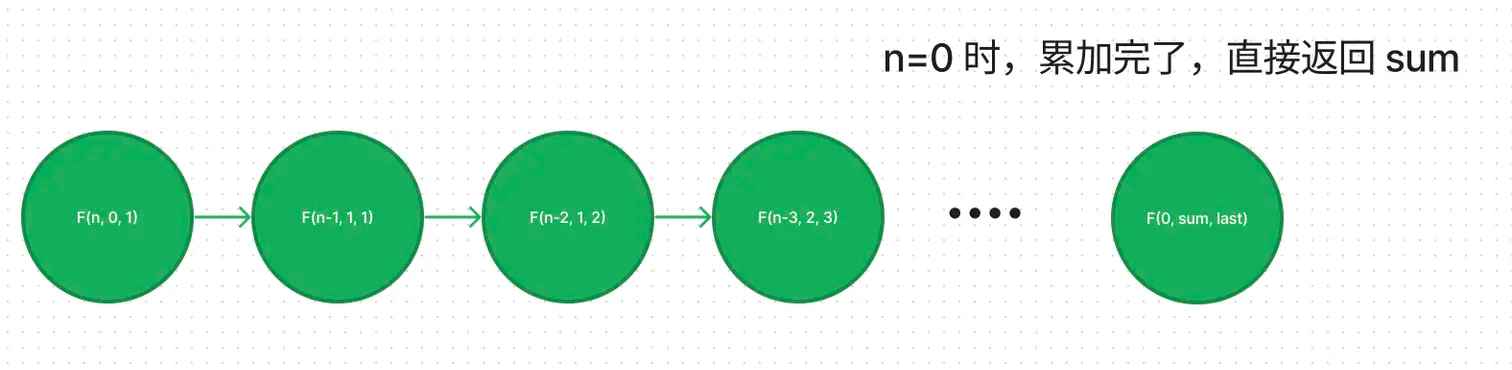
image-20230713155213815

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 函数中多了两个参数不太优雅？传个参数默认值就可以解决！
function fibonacci(n, sum = 0, last = 1) {
  if (n === 0) {
    console.log(sum)
    return sum;
  }
  return fibonacci(n - 1, last, sum + last);
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
// ...
fibonacci(50)

3. 手法优化——循环实现

3.1 普通for循环

使用普通的 for 循环实现斐波那契数列，只需要将前两个数字作为起始值，每次循环加上前两个数字的和，即可实现斐波那契数列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function fibonacci(n) {
  const arr = [0, 1];
  for (let i = 2; i <= n; i++) {
    arr[i] = arr[i-2] + arr[i-1];
  }
  console.log(arr[n])
  return arr[n];
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
// ...
fibonacci(50)

3.2 空间上的优化

就是省一个数组，如果只求第n个的值，也就没有必要用数组保存了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function fibonacci(n) {
  let sum = 0;
  let last = 1;
  for (let i = 1; i <= n; i++) {
    const tmp = sum;
    sum = last;
    last = tmp + last;
  }
  console.log(sum)
  return sum;
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
// ...
fibonacci(50)

3.3 ES6解构赋值

上面的代码看的有些许难受，因为循环的时候引入了一个临时变量tmp，其实我们用ES6中的解构赋值代码可读性会更好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function fibonacci(n) {
  let sum = 0;
  let last = 1;
  for (let i = 1; i <= n; i++) {
    [sum, last] = [last, sum + last]
  }
  console.log(sum)
  return sum;
}

// 验证
fibonacci(0)
fibonacci(1)
fibonacci(2)
// ...
fibonacci(50)

3.4 ES6 Generator 函数写法

ES6 中的 Generator 函数是一种可以在函数调用时，暂停和恢复运行的函数。
Generator 函数返回的是一个迭代器，因此可以使用 for…of… 语法进行遍历。for…of… 循环可以自动遍历 Generator 函数运行时生成的 Iterator 对象，从而不需要再调用 next 方法。这样，就可以对 Generator 函数中 yield 生成的数据进行处理。
是不是发现了：这里使用 Generator 函数和 for…of… 来写斐波那契数列也挺合适。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function* fibGenerator() {
  let [prev, curr] = [0, 1];
  while (true) {
    yield prev;
    [prev, curr] = [curr, prev + curr];
  }
}

function fibonacci(n) {
  let index = 0;
  for (let value of fibGenerator()) {
    if (index++ < n) continue;
    console.log(value);
    return value;
  }
}

// 验证
fibonacci(0) // 0
fibonacci(1) // 1
fibonacci(2) // 1
fibonacci(3) // 2
fibonacci(4) // 3
fibonacci(5) // 5
// ...
fibonacci(50) // 12586269025